加沢知毅(東京大学先端科学技術研究センター)
サプリメンタリー1:神経細胞の構造
S1.1 昆虫の神経細胞
神経細胞は細い管のような形状が分岐した木構造のような形状をしている(図S1-1)。その根元には細胞核の存在する細胞体があり、遺伝子情報や蛋白質をそこから供給している。多くの昆虫の神経細胞は単極性(細胞体から一本のneuriteがのびている)であり、哺乳類の神経細胞の多くが双極性(細胞体から二方向にneuriteが伸びており、一方は入力側でdendriteと呼ばれ、一方はミエリン鞘につつまれた軸索(axon)を通して出力にむかう(図S1-1の錐体細胞))もしくは多極性であることは異なる。しかし、例えば昆虫培養神経細胞では双極性や多極性の神経成長が観察できることとから、それは神経細胞の情報処理メカニズムというより、昆虫の発達機序により細胞体が体の表面にあることからの制約が多く寄与していると考えられる。

図S1-1 神経細胞
左上 昆虫触角葉出力神経。上中央 LALといわれる神経叢で分枝をもつ昆虫介在神経。上右 哺乳類錐体細胞(牛丸+2012)。左下 ケンヨン細胞のSIZ(Trunova+2012) 右下 哺乳類細胞のSIZ(Leterrier2016)
SIZ: スパイク発生箇所 (spike initiation zone)
昆虫の神経細胞の一個一個はミエリン鞘につつまれておらず無髄である。ただし、局所神経回路をなしている密集ニューロパイル(神経叢)やそれをつなぐ神経路は全体としてグリア細胞で包まれているので、必ずしも外部環境と自由に接続しているというわけではない。
リン脂質二重膜からなる細胞膜の抵抗は非常に高く(>106 ohm /cm2)、電気的にはほぼ絶縁体とみなせるが(花井、1972)、細胞膜上には、イオン選択性をもつイオンチャネル等のイオン輸送タンパク質が存在しており(図S1-2)、よりマクロ的に見ればある程度の電気的導電性が常にあるとみなせる。なお細胞内の導電率はその細胞質のイオン組成から計算されるものよりはるかに低く細胞内の高分子や脂質膜をもつ細胞内小器官がおおいに影響している。イオンチャネルはアゴニストの結合や、膜タンパク質内の膜電位センサ、またその他分子的修飾をうけた制御の下でコンフォメーション変化をおこし、その開閉確率を変えることが動的な情報処理を基礎づけている。
S1.2 細胞の電流機構
細胞内のイオン環境は細胞外と異なるイオン組成になるが恒常性が保たれている。言い換えれば化学ポテンシャルとしてエネルギーをため込んでいる。イオンチャネルはその通すイオンの選択性をその電荷と疎水性に基づいて持つことで(Hille, 1992)、個々のイオンの濃度差の化学ポテンシャルを電気化学ポテンシャルの源、すなわち電池として利用することが可能であり、神経細胞はこれを情報処理の駆動力として利用する(図S1-2)。
神経細胞内外のイオンチャネルの選択性においては、静止活動時には主にカリウムイオン(K+)の電気化学ポテンシャルが支配的であり、細胞内のカリウムイオンが濃くなっていることにより、昆虫神経細胞では-50mV超の内外電位差が生じる。信号伝達のためには、細胞外において主にNa+イオンが内側よりも濃いことによって保たれ、それより生じる逆むきの電気化学ポテンシャルを用いる。その他クロライドやカルシウムイオンなども膜電位に影響を与える。
なお神経生理学ではこの膜電位がさらに深くなる方向を過分極、浅くなる方向を脱分極と称する。また、細胞外電位を通常0電位として扱い、細胞の外向きに流れる電流を正とする。
個々のイオンチャネルは通例10-100 pS程度のイオンコンダクタンスを持つ複数の膜タンパク質の複合体である(Hille, 1992;曾我部編, 1997)。また、細胞膜上にはより小さな単一コンダクタンスをもつイオントランスポータやATPポンプなども存在するが、これらはゆっくりした制御でイオン濃度バランスを保つ機能が主であり、情報処理としての役割は小さいと一般的には考えられている。計算モデル上では細胞膜の静的なリーク電流としてまとめられることが多い。イオンチャネルは細胞膜上でゆっくりと拡散するが、膜の細胞骨格と弱い結合があり、また特定部位に拡散が妨げるフェンスにより、局在する(藤原, 2005; Choquet+, 2003; Heine+, 2016)。特にスパイク発生部位には電位依存性のNa/Kチャネルが局在する(久場, 2018; Rasband+, 2010; Ravenscroft+, 2020)。報告されているイオンチャネル分布データでは、境界が存在し、一定領域内においては定常的な量の存在が示唆されていることから、イオンチャネルの分布密度は領域内において一定とした計算モデル、すなわち膜へのタンパク質の湧き出しが小さく十分な時間が立っているために拡散の結果領域内は定常状態に達しているという計算モデルを筆者らは用いている。
なお、触角葉局所介在神経の活動にははっきりした入力部と出力部がほぼ観察されていないことから、筆者らは全体を均一なものとして扱っている。開状態と閉状態をある遷移確率で行き来しているイオンチャネルの開閉の速度論的解析は、歴史的には主にパッチクランプ法による単一チャネルレコーディング(Sakman+, 1983)によって調べられており、多くのイオンチャネルではその複数の閉状態とひとつの開状態を行き来するマルコフ連鎖モデルとして速度論的に記述されている(ただし、現状の電気的記録方法の技術的限界からサブミリ秒の領域には不明な部分が多く残っていることも詳細なダイナミクスを検討する場合留意すべきではある)。また、げっ歯類神経系などと比べると研究者人口の問題から昆虫特有のイオンチャネルの挙動の理解についてはそのはまだ十分とは言えないが、遺伝的解析が可能なためショウジョウバエのイオンチャネルは単体の動物種としてはよく調べられている。
1つの神経細胞内の入力から出力への情報伝達は、主に電気的な情報処理が行われる。大部分の神経細胞ではスパイク状の活動電位を発生させ、そのneuriteにそって伝搬させることによって、後シナプスから次のシナプス前末端まで情報が伝達される。いわば、アナログ信号のデジタル信号への変換である。一発の活動電位が発生する基本メカニズムは哺乳類と同じであり、イカ巨大軸索においてホジキン・ハックスレイが解明したメカニズム(Hodgkin,& Huxley, 1952 )そのものである。すなわちある程度の脱分極がおこった状態で電位依存性Na+チャンネルの電位上昇(脱分極)に対する正帰還と、それに遅れるK+チャネルの過分極による負帰還により結果としてインパルス状の電位が発生する。空間的には同様のプロセスが遅れてより遠方で繰り返されて、ソリトン(孤立波)としてスパイク状の電位が伝播する。これは活動電位と称される。アナログ電位からのスパイク発生においては、その他(間接的であっても)電位依存性のよりゆっくりとした脱分極・過分極性のチャネルが、スパイクは発生頻度調整に大きな役割を果たし(林, 1992)、アナログ信号からデジタル信号へのスムーズな変換が行われる。
大部分の神経細胞では、スパイク状の活動電位を発生させて、そのneuriteにそって伝搬させることによって後シナプスから次のシナプス前末端まで情報を伝えることになる。スパイク発生箇所 (spike initiation zone (SIZ))は、双極性の哺乳類神経細胞ではaxon initial segment(AIS)とよばれる細胞体直近のアクソン側部位にあるが(図S1-1)、昆虫神経細胞の単極性神経では細胞体からのneuriteがmain neuriteが交差した場所の出力側にあるらしくKenyon細胞でその様子が確認されている(図S1-1; Ravenscroft+, 2020; Trunova+, 2011)。
S1.3 神経回路の末端の細胞
神経系の入力末端には感覚受容細胞 (sensory receptor cell) が存在する。感覚受容細胞において、光や化学物質、振動など様々なモダリティの情報は、受容体膜タンパクが受け取り、イオンチャネルにその情報がつたえられることでイオンチャネルの開閉確率が変わり、アナログ信号である情報変換電流に変換される。この情報変換機構には順応があり、一定の信号に対する応答が時間的に減少することでダイナミックレンジを適応的に調節することができる。その情報変換機構と調節機構は情報モダリティによって様々であり、哺乳類と昆虫でも幾分異なるが、cGMPやcAMP、そして七回膜貫通型膜タンパクが大きな役割を果たすなど、哺乳類と昆虫間では分子機構の上で多くの類似性をもつ。
また、昆虫においては感覚毛という感覚器があり、そのなかに嗅覚・味覚・機械感覚の感覚細胞が存在しているのは特徴的である。感覚受容細胞の情報変換は、一般の神経細胞の後シナプス電流と同様の仕組みであり、最終的にはシナプスを通じて次の神経細胞に情報が伝達されていく。神経回路の出力側の末端である筋肉には、神経筋接合部を介して伝達される。神経筋接合部のプレ側は通常のシナプスであり、ポスト側は筋肉があり、ポストシナプス電流の発生の結果おこるカルシウム上昇がトリガーとなり筋肉の収縮がおこる(Wicher+, 2001)。
サプリメンタリー2:シナプスの構造
S2.1 シナプス -神経細胞間の接続-
神経細胞同士が接合し、インタラクションする部位をシナプスと呼ぶ。歴史的には、シナプスの存在は最終的に電子顕微鏡観察で同定されることで(Robertis+, 1955; Palade+, 1955)、確固たるものになり、今でも電子顕微鏡での観察が信頼できる確認手段だが、共焦点顕微鏡でもその位置を推定することは可能である(図S2-1)。
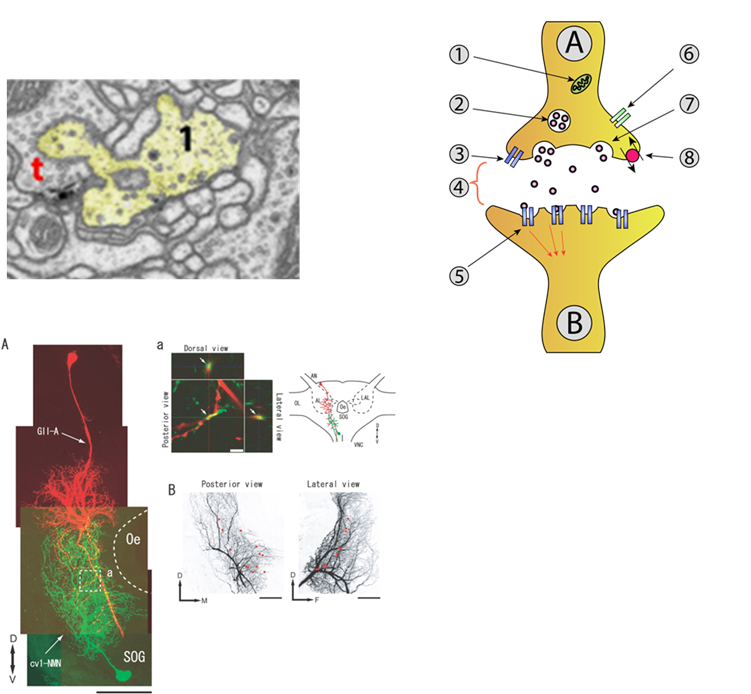
図S2-1 化学シナプス
左上 昆虫シナプスの電験画像(Petralia+)tはTバーと呼ばれる前シナプス特徴的な構造) 右上シナプスの模式図(wikimediaより)Aニューロン(シナプス前) B:ニューロン(シナプス後)1ミトコンドリア 2神経伝達物質でいっぱいのシナプス小胞 3自己受容体 4シナプス間隙 5神経伝達物質受容体 6カルシウムチャネル 7神経伝達物質を放出する融合小胞 8神経伝達物質再取り込みポンプ
左下 光学顕微鏡によりシナプスの同定 赤と緑はそれぞれ蛍光染色した昆虫の神経 3次元的な重複によって(a)シナプス位置が推定される(Bの赤点)
シナプスは、電気シナプスと化学シナプスに分類される。現代ではシナプスと呼ぶと化学シナプスを指すことが多い。電気シナプスは、二つの細胞の接合部に二つの膜タンパクが向かい合わせて接合する構造をしており、場合によって整流性はあるものの、基本的には二つの細胞を受動的に抵抗で連結しているのであり、両者の膜電位を平均化する方向で働く。無脊椎動物では電気シナプスは比較的多いが、コネクト―ムでも電気シナプスまで追っている事例は少なく、その情報処理に対する寄与が明確に示されている例は少ないため、本稿では化学シナプスについてのみ記述する。
神経細胞の出力末端には(化学)シナプスがある。シナプス前末端では活動電位の到達を受けてカルシウムチャンネルを通したカルシウムの流入がおこる。その結果として何段階かの時空間的な反応を通して神経伝達物質がシナプス前末端から放出される。シナプス後膜には、神経伝達物質を受容するレセプタ分子が存在し、情報伝達経路(大部分のシナプス後膜に存在するレセプタ蛋白質はイオンチャネル-レセプタ複合体である)を介して、シナプス後膜のイオンチャネルの開閉状態が変化し、膜電位が変化する。哺乳類脳内の興奮性シナプスの主な伝達物質はグルタミン酸であるが、昆虫脳内においては主にアセチルコリンである(Osborne, 1996)。脊椎動物と筋肉と脳で役割が入れ替わっているところが興味深い。GABAが主な抑制性の神経伝達物質である点は哺乳類と同様だが、興奮性のGABA受容体も存在は確認されており(Shimizu+, 2017)、局所回路のなかでは必ずしもその類推は正しくないことも注意は必要である。ニューロモデュレータと呼ばれる生体アミンや小ペプチドは、後シナプスで直接高速にイオンチャネルの開閉を制御するのではなくて哺乳類と同様に細胞内代謝系を経由した情報伝達に関与すると考えられている。生体アミン分子では、5HT、ドーパミンなど哺乳類と共通したものが多いが、昆虫ではoctopamineも重要な役割をはたすということが知られている(Nässel, 2002; Kim+, 2017; Damme, 2021)。
S2.2 シナプス小胞の放出機構
シナプス前末端には神経伝達物質の放出メカニズム(放出装置:The Synaptic Vesicle Release Machinery )があり、その実体は小胞と細胞膜をつなぐSNARE複合体(soluble NSF attachment protein receptor complex)とよばれるタンパク質群を中心に構成されている(図S2-2)。カルシウムイオンチャネルから流入した急速なカルシウム上昇にひきつづき、放出装置内のタンパク質とカルシウムイオンの結合がトリガーとなり、RRP(readily releasable pool:膜に接合している即時開口放出可能な小胞のストックを指すが基本的には生理的な概念:Kaeser+, 2017)として存在する小胞が前末端の細胞膜と融合して開口することにより多数の神経伝達物質がシナプス空隙に放出される。SNARE構成タンパクにはいくつかカルシウム結合がみられ、放出とその速度調節(Neher+, 2009)に関与している。サブミリ秒からミリ秒スケールの拡散によって、神経伝達物質は後シナプスの神経伝達物質の受容体まで到達し、その後シナプス間隙からは分解や取り込みのより除去される。ポストシナプス電流はこのダイナミクスと受容体タンパク質の順応との複合により、素早い脱分極(過分極)にひきつづき、ベースラインにゆっくりともどるタイムコースをたどることになる。
放出装置は小胞上、細胞膜上、そしてその間をつなぐ複数のタンパク質から成っており(Rizo+, 2015; Motida, 2022)、速度論的化学反モデルも提案されているが(たとえばPan+, 2009)、個別のシナプスにおける多段階の結合乖離の反応と細胞内メッセンジャーの拡散・移動を含むため分子機構と実際の現象とはまだ十分には説明できないのが現状である。
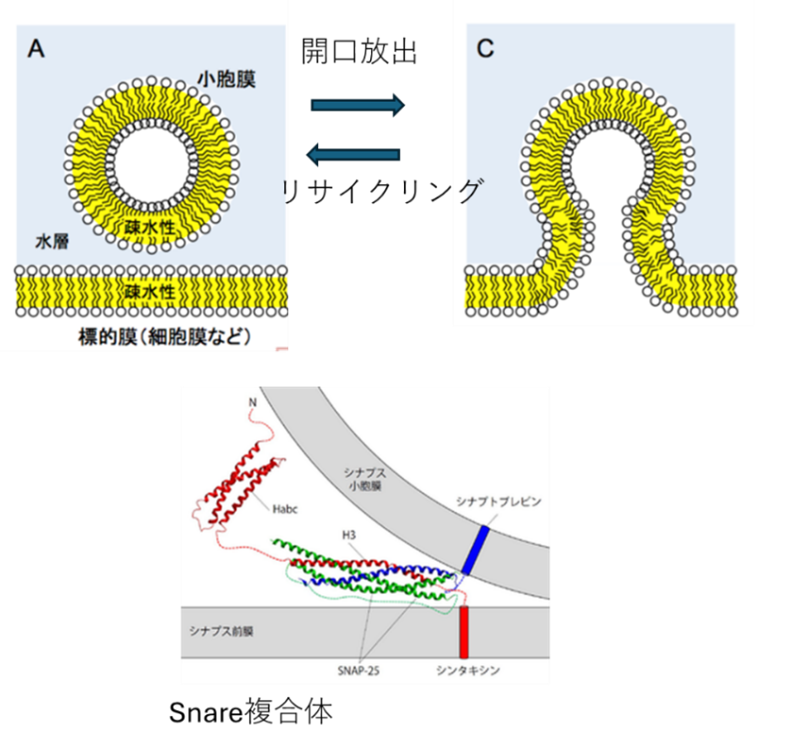
図S2-2 シナプス前末端の放出メカニズム
上 開口放出(高橋2016)シナプス小胞は膜に接合し、融合することで開口放出する。その小胞はエンドサイトーシスで再び小胞にもどり、再回収・再合成された神経伝達物質が充填され、再び放出部位に運ばれる。
下 放出装置の分子機構のSNARE複合体を主眼とした模式図(西木2015)SNAREが細胞膜側と小胞側をつないでおり、エキソサイトーシス/エンドサイトーシスを制御する。
また、刺激がない状態でもシナプス前末端では自発的な開口放出が存在し、その結果としてmPSC(miniature postsynaptic current)とよばれる後シナプス電流が観察され、前末端のカルシウム濃度依存性があることが知られている(Hubbard, 1961)。放出後シナプス小胞はリサイクルされ endosomesにいったん回収され、神経伝達物質等が再充填されたあとにRRPに再び運ばれる。シナプス後膜では多くの場合、シナプス受容体蛋白質がチャネルレセプター複合体として存在する。神経伝達物質がチャネルレセプター複合体に結合することによってそのイオンチャネルとしての開確率が上昇し、そのイオン選択性に従い興奮性もしくは抑制性としての信号になる。
サプリメンタリー3:シナプスと学習
S3.1 シナプス可塑性概論
シナプス可塑性とは、シナプス前末端に到達するスパイクあたりの後シナプス電流の大きさが変化することを指す。この物理的基盤は前述の放出装置と後シナプスのイオンチャネルである。 これらはその変化が減衰する時間的スケールによって、短期可塑性(Short-term plasticity)や長期可塑性(Long-term plasticity)と分類される。 短期可塑性は多くの場合シナプス前末端のカルシウムイオンの挙動が関係している。細胞外のカルシウム濃度は1mMオーダーだが、細胞内では100nMオーダーと一万倍の極端な濃度差があり、イオン輸送機構とともに細胞質内のカルシウム結合蛋白質や細胞内小器官によって細胞内の恒常性が保たれている。またこの極端な濃度差のため、カルシウム流入があった場合、時空間的に極度に偏った分布をすることになる(Zucker+, 2002; Regehr, 2012; Ohnuma+, 1999)。
シナプス前末端に活動電位が到達するとカルシウム流入がおこり、開口放出がおこる。放出装置には短期可塑性に関わるカルシウムセンサが存在している。しかし、このカルシウムは短時間では完全に排出されず、シナプス前末端の細胞質におけるこの時空間的に変化する残存カルシウム(residual calcium)が短期増強の原因となる。すなわち、上記のバッファとの相互作用で時空間的に複雑な減衰とカルシウムセンサとのインタラクションからなる過程が細伝達効率の変化を引き起こす。短期可塑性のもっとも早い部分は前の刺激で上昇したカルシウムがつぎの刺激までに除去しきれないカルシウム濃度のダイナミクス(残存カルシウム説)でほぼ説明できるが、その他の過程もや、カルシウム非依存性のものもある(Regehr, 2012; 木島+, 1992)。

図S3-1 シナプス可塑性とそのモデル
1 EPSP(excitory post synaptic potential)でみた短期・長期増強の違い(Wang+2020)短期増強は有限時間でベースラインに回帰する。
2 スパイクタイミング依存性可塑性(模式図): STDP関数は、シナプス前スパイクとシナプス後スパイクの相対的タイミングの関数として、シナプス結合の変化を示す(Sjöström+2010)
3 BCMルール yはシナプス後の活動強度、Φはシナプス強度の変化、θMは修正閾値である。θMは活動履歴によって修正される。(Blais+2010)
シナプス小胞は再び細胞に取り込まれたあと、いくつかのプールを通って輸送されながら神経伝達物質が最充填されリサイクルされる。短期抑制(Short term depression)は、RRPもしくはそこに小胞を供給するいずれかのステップの枯渇もしくは抑制ととらえられる。
長期可塑性のうちLTP(long term potentiation 長期増強)においては、後シナプス部位でのカルシウム濃度上昇をきっかけとして、後シナプスのチャネルレセプター複合体の神経伝達物質の感受性、長期的には分子数まで増加する分子メカニズムが注目され、グルタミン酸シナプスで特によく研究されている。また、逆方向メッセンジャーによってポストシナプスからプレシナプスへの情報伝達もおこる(Regehr+, 2009)。これは後述するヘッブ則の物理的基礎として考えられる。
<<<以下? 要説明: また頻回刺激頻度に依存したシナプス前末端でのnon-Hebbian potentiationも存在し、生理的な性質もよく研究されている。それとは別に恒常性維持などのためにシナプス前後において分子比率や競合シナプスの中でその数や比率を調整するsynaptic scalingやメタ可塑性も存在していることが知られている(Vose+, 2017)。トップダウンの観点ではそれらを短期過疎性に組み入れて除外するか、あるはホメホスタシス機構の一種として分けて考えられることが多い。>>>
S3.2 トップダウン可塑性モデリング
前シナプス末端での頻回刺激がシナプス効率を変化させることは神経筋接合部をはじめ多くのモデルシナプスで見いだされ、その動作理解の基礎となり、特に一時的な効率変化である短期可塑性においてはおおきな成果をあげた(Del Castillo+, 1954; Katz+, 1968; Dobrunz+, 1997)。また神経回路において単一シナプスを観察するとき、Hebb則として知られているものが見いだされた(Hebb, 949)。この挙動は「細胞Aの軸索が細胞Bを発火させるのに十分近くにあり、繰り返しあるいは絶え間なくその発火に参加するとき、いくつかの成長過程あるいは代謝変化が一方あるいは両方の細胞に起こり、細胞Bを発火させる細胞の1つとして細胞Aの効率が増加する。」とHebbは記述している。要約すると、「一緒に発火する神経細胞をつなぐシナプスは強化される」となる。また単一シナプスの系で前シナプスを頻回刺激するとき、その頻度によって後シナプスに増強 や抑圧がおこることが観察され、シナプスの安定も考慮された長期可塑性のCooper-Liberman-Oja理論(Cooper+1979)として、またそれをさらに動的にしたBCM(Bienenstock-Cooper-Munro)ルールとしてまとめらえた(Bienenstock+, 1982)。すなわち、過去の履歴の結果としての後シナプスでの活性度に依存してシナプスpotentiation やdepressionの閾値が変化し、全体の活動が安定化する方向にはたらくとされ、この理論がもたらす予想はいくつかの系で確かめられている。
さらに別の形でHebbian ruleに近いものがみつかった(Markram+, 1997)。頻回刺激ではなくてシナプス前細胞と後細胞のそれぞれ一発の活動電位を組み合わせた刺激を連続して与えることでLTPやLTDを誘導することができるのである。それがSTDPである(Bi+, 1998)。STDPにおいてシナプス前側のスパイクの後にシナプス後側のスパイクが発生するとシナプスが強くなり、シナプス後側のスパイクの後にシナプス前側のスパイクが発生するとシナプスが弱くなることで抑圧と増強がある程度バランスされる。
その後、BCMルールとSTDPルールは後シナプス側がある程度の頻度の活動電位を受けているような条件でほぼ同等ものとして動作することも知られている(Izhikevich, 2003; Toyoizumi+, 2008)。また、昆虫キノコ体のKenyon 細胞からキノコ体出力細胞に向かうシナプスでもSTDPが観察された(Cassenaer+, 2007 )。これは大きなトピックであり、STDPが標準的な長期可塑性の機構の一つという認識が今や共有されるようになった。
このように可塑性の現象論から分子論に至る研究が様々に展開されるなかでは、これら全体を統一的に説明できる原理はまだ知られていない。しかし、その有力なものをひとつあげるなら、情報処理能力とエネルギー消費を按分させてその最適化を考える自由エネルギー最小化の概念であり(Friston, 2009 )、STDPルールに類似のものへも変換できることがわかっている(Isomura+, 2016)。また、現象論として発見されたSTDPやBCMルール(後述)は学習にかかわる可塑性と恒常性を考慮した上で発散消失しないシナプス可塑性に対しる一つの基礎づけとなっている。
サプリメンタリー4:GPEAモデル(Belmabrouk+2011)
S4.1 マルチコンパートメントHodgkin-Huxley型モデルへ
神経細胞と神経回路のふるまいを計算モデルに落とし込むのはどのようにすればいいのか?
筆者らは生物物理学的詳細モデル(biophysically detailed model)としてのマルチコンパートHodgkin-Huxley型モデルによる定式化を採用しているが、そこに至るまでを、またその周辺の部分を説明する。

図s4-1 神経細胞とマルチコンパートメントモデル
左 単純化した神経細胞の発火の仕組み。受容体や後シナプスの可変電流をうけ、パッシブに近いdendriteを通して信号が伝わりSIZで発火がおこる。
右 右細胞形態を有限個のノードのつながりとして近似して、各ノードの電位とノード間をつなげるシリンダーを流れる電流を計算して統合する。
神経細胞が電気的に情報処理を行うためには電気的なエネルギーが必要で、神経細胞は細胞内外に特定のイオンの濃度差をつくることで電気化学的ポテンシャルを蓄えている。
電気化学的ポテンシャルはネルンストの式で表すことができ、あるイオンXについて
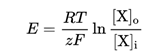
となる。これは特定のイオンに対する選択的な透過性に対して細胞内外濃度の違いに応じて電位差が生じることを意味しており、特定のイオンしか通さない場合においてはイオンチャネルの抵抗を与えればこれで膜電流が計算できる。すなわち、各イオン毎に発生する電位を足しあわせればよいわけだ。
ただし、物理的性質を勘案すると、膜内のイオン移動経路の電場変化が均等であるという仮定(等電場仮定)をおくとイオンの移動度から、その電気化学的ポテンシャルを計算することが可能となる。それがGHK膜電位方程式(Goldman-Hodgkin-Katz voltage equation)である。
GHKの仮定下で、例えば細胞膜を透過するイオンがK+、Na+、Cl-のみならば、そのときの平衡電位は

とあらわすことができる。ここでPxはそれぞれのイオンの物理的易動度から計算される透過係数である。
これに基づいてイオン電流まで計算するなら、
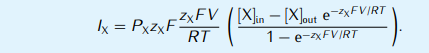
となる(GHK電流方程式;GHK current equation)。だが、この記述は煩雑で計算量もむやみに重くなるため、詳細に1細胞の電気的ダイナミクスを扱う場合は、イオンチャネルの平衡電位だけを用いて(そうしないと内外濃度差が酷く大きいカルシウムなどで事実に反する値がでてしまう)、もしくは平衡電位の実測値を用いてイオンチャネルを一定の抵抗と電位エネルギをもつものとして扱い、それらを細胞の形態の電気回路を記述したケーブル方程式に入れ込む等価回路モデルとして扱われることがほとんどである。
ケーブル方程式は次のように書き下すことができる。
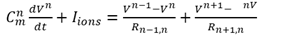
この式はケーブルとして紐のようなものとして表現された神経細胞がその両側に影響されることを示している。
(通常の場所では式にあるように隣接のコンパートメントとの2つの接続項だが、枝分かれ場所(図4-1右の2.0)では三つ、端点(図S4-1右の0.0 4.1 5.0)では一つになる)
ここでCmはコンパートメント毎の膜容量でありIionsはその場所でのイオンチャネルの総和によるものであり、複数のチャネル電流IchXを用いて

と記述できる。なお

である。EchXはそのイオンチャネルの平衡電位である(理論的にはイオンチャネル毎の各イオン透過度をあてはめた上での上記のEmに相当する)。
また軸索抵抗Rjkは隣り合ったiとjのコンパートメント間の抵抗。vi vjはそれぞれi番目、j番目のコンパートメントの電位を意味する。
静的な膜抵抗はこの場合リーク電流としてあらわされる。これが等価回路的な扱いである。
なお、連続空間で考えるなら、
単位長さあたりの抵抗rl ( Ω/m)は
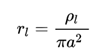
(aはケーブルの半径 ρlは比抵抗)
と計算可能で、空間的にも指数関数的に電位変化が減衰する。
わかりやすく。無限長の枝分かれなしのケーブルで考えると
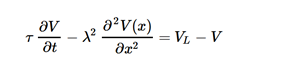

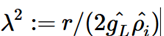
である。このτを膜の時定数(membrane time constant)、λを長さ定数(length constant)と呼ぶ。
ケーブルが均等な場合全体にスパイク上の電位変化がおこれば、τに従って時間的に指数関数的に減衰する。また、一点で電流注入があり続ける時、定常解は

とあらわすことができ。ラムダの長さで1/eだけ電位信号が減衰することがわかる。
ただし、これは受動的なケーブルに対する理論であり、実際の神経細胞では、後シナプス電流として入力を受け取り、それが減衰されるまえに統合されてスパイクとしてデジタル的な信号に変換され、出力部位としてカルシウム濃度の局所的な上昇を通じてシナプスの開口放出を引き起こす。
この核心的な部分はオリジナルなHodgkin-Huxley方程式で、ヤリイカ巨大軸索においてこのモデルはつくられ、その正しさが確かめられた(Hodgkin+, 1952)。すなわち

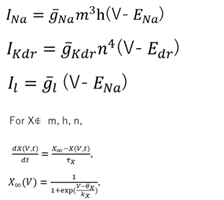
である。ここでm, n はナトリウムチャンネル、カリウムチャネルの活性化ゲートで、hはナトリウムチャネルの不活性化ゲートである。急激な電位上昇が生じたときにその活性度の上昇はm>n>hの順でおこることがスパイクの発火を形づくっている。このように電位依存のイオンチャネルの挙動を膜の局所で記述して、ケーブル方程式でつながれたものをマルチコンパートメントHodgkin-Huxley型モデルと称する。なおここまでに用いられた基本的な電気生理学の概念(ネルンスト式、GHK式、等価回路モデル、ケーブル方程式 Hodgkin-Huxley方程式など)については、宮川ら(宮川+, 2003)に詳細な解説がある。
電位依存性のナトリウムチャネルと カリウムチャネルが一種類ずつあれば、スパイク発生自体は説明できるが、その発生頻度を電流にあわせて調節するには電位依存性の脱分極性と過分極性のチャネルが別にあることが望ましい(Hayashi+, 1992)、そのようなものの候補としてよりゆっくりとした制御を受けるカルシウムチャネルやポタシウムチャネルが存在する。筆者らはガに注目し、そこに組み込まれたカルシウム感受性Kチャネルを含む、Hodgkin-Huxley型モデルである、GPEAモデル(Belmabrouk+, 2011)を主に採用している。
すなわち
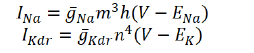


であり、 さらにカルシウム濃度として



としている。多くのイオンチャネルモデルより、生物物理学的に相対的に忠実なため筆者らは昆虫神経系機能シミュレーションでは、主にこれを用いている(Kazawa+, 2019; Higuchi+, 2022)。ここでは スパイク発生に付随して流入カルシウムに反応するカルシウム依存性カリウムチャネルのふるまいが記述されている。ただしこれは細胞内カルシウム動態の見地からすると荒い近似であり、細胞内のモビルバッファとインモビルバッファとの結合乖離を繰り返す細胞内カルシウムの時空間的なふるまいを詳細な記述(Rüdiger, 2014; Matthews+, 2015)する必要のあることは注意されたい。
昆虫においてはスパイクに関与すると思われる電位依存性ナトリウムチャネル遺伝子は、カイコガでもショウジョウバエでも一つしかない。カリウムチャネルについては複数ある。ただし完全にナトリウムチャネルとはいえないがカルシウムをもよくとおすDSC-1チャネル(Castella+, 2001)も存在する(Rinkevich+, 2020)。
S4.2 その他の神経細胞モデル
複雑な単一細胞の動態を説明するのに十分な詳細を盛り込むことと、モデルを扱いやすくするためにこの複雑さを減らすことの、そのラインの元には様々な神経細胞モデルが存在し(Herz+, 2006)、筆者らが採用しているマルチコンパートメントモデルはそのなかでももっとも詳細なものの一つある。ここではそのなかでもより計算量の少ない神経細胞モデルについて触れておこう。
哺乳類の神経細胞では細胞体ホールセルクランプによりスパイク発生部位がその近傍のイオンチャネルの性質の実験データが手に入りやすいことから、スパイク発生だけに注目したHodgkin-Huxley型のシングルコンパートメントとして扱われることがある。しなしながら、このモデルでは神経細胞の形状を考慮しないことにより、細胞のキャパシタンスやシナプス信号を受け取った後の軸索(ケーブル)での減衰や統合、またシナプス出力までの遅延などにおいて非現実的で広い適応を阻害するモデルになる可能性がある。
そのためスパイク発生を物理学的な現象と扱わずに一つのイベントとして割りきる考え方がある。その流れで提案されているのが(Leaky)Integrated-and-fire(LIF)モデルとその派生モデルである。極端なものではスパイク発生閾値をかなり自由に変動させることで自然のスパイク発生にあわせるAdaptive exponential integrate-and-fire Leaky integrate-and-fire(Gerstner, 2009)やmulti-timescale adaptive threshold (MAT) neuronal modelモデル(Kobayashi+, 2009)まで存在する。
LIFモデルはパッシブな膜と閾値をトリガーとする不連続な変化を決定論的に

と記述される。すなわち、電位が閾値になったとき膜電位がリセットされるが、これを瞬間的にスパイクイベントが発生されたと記述する。神経活動が静的な場合は閾値が存在するという前提であり、神経ネットワークでも多くの理論的解析がなされている。また、これを拡張した例えばMATモデルは不応期に対応する閾値変化を複数の指数関数の和として記述したモデルであり、ニューロンの発火パターンの再現度は非常に高い。
他に有名なものとしてIzhikevich モデルがある。これはHodgkin―Huxleyとintegrated-and-fireの折衷案であり、計算負荷が高い部分をintegrated-and-fireとして記述する。
dv/dt = 0.04v² + 5v + 140 − u + I(t)
du/dt = a(bv −u)
V:= c, u:= u + d If v => p,
Izhikevichモデルのチューニングは敷居は高いが、計算負荷の高い部分を省略しつつスパイクパターンをある程度近似できるメリットがある。
その他、スパイク発生の非線形性力学的特徴に着目してHodgkin-Huxley方程式を簡略化してモデリングする系統のモデルもある。Morris–Lecar モデル(Lecar, 2007)や FitzHugh-Nagumoモデル(Izhikevich+, 2006)などがそれにあたる。なお、この種のスパイク発生モデルをマルチコンパートメント化する場合。(Izhikevich+, 2008)のようにスパイク統合までの過程に受動的なケーブルをいれてモデル化する場合がある。
ANN(artificial neural network)に使われるANNニューロンモデルについても記述する。このモデルは同等神経の集合的な活性度を連続変数として記述される。

このモデルは通常、細胞の状態に時定数がないとものとして簡略化して離散時間でシナプスを設定する。出力関数はいくつかのものがあるが、古典的には閾値モデルのシータ関数ですなわち

である。これはMculloch-Pittsモデル(McCulloch+, 1943)とよばれる論理演算モデルのものである。その後Hopfieldによって生物的にはミカエルスメンテン出力関数を採用した連続量モデルが採用になり(Hopfield, 1984)、これが第二次人工知能ブームのきっかけとなった。
これは例えば、

と記述される。
なお、近年の深層学習ANNでは線形性に最小限の非線形をまぜこむMAXOUT関数の一種であるReLU (Rectified Linear Unit, Rectifier)が使われており、その場合

となる。
S4-3 シナプスモデル
シナプスモデルにおいて確率的なモデル記述(二項分布に従う個々のシナプス小胞の振る舞いを記述する)もあるが、ここでは決定論的なモデルについて解説する。
前シナプスにスパイクが到達したときにそのスパイク変化する電位変化に駆動されて電位依存性のカルシウムチャネルが開きカルシウムが流れ込む。そのタイミングだけをイベントとして取り出し、後シナプスにあるコンダクタンスを駆動させればシナプスの基本モデルとなる。すなわち、

と定義する(ただしt simは全体のシミュレーション時間 tspike_nth はシナプス前末端へのn番目のスパイクの到達時間 Δtは神経伝達物質の拡散によるシナプス遅延である)。このときスパイクの出力関数、SYOUTを
If t<0
SYOUT=0
If t>0
SYOUT=w f(t)
と記述する。このときwはシナプス荷重で、fはシナプス出力波形関数であり、
fex1=exp(-t/τ)
fex2=t・exp(-t/τ)
fex3=exp(-t/τ1 )+ exp(-t/τ2)
と設定する。この場合可塑性は、シナプス荷重wの変化として別に設定し、スパイクの履歴による短期可塑性、もしくはシナプス前後の関係を使いSTDPルールで記述できる。
S4-4 マルチコンパートメントモデルよる複雑モデル
より詳しいモデルではイオンチャネルの揺らぎを確率論として計算することになるが、これはランジュバン方程式として集合的な確率を乱数ノイズを用いて計算することもでき、正確なシミュレーションが可能である(Goldwyn+, 2011)。このように確率論をシミュレーションに導入すると活動にバリエーションがでる結果、平均した伝達関数としてみた場合の入出力の勾配がゆるやかになる傾向がある(図S4-1)。
勿論より複雑な細胞モデルは、考えうる3次元格子を用いて膜を構成し、物質の移動と化学反応をシミュレーションすればいい。細胞内のカルシウム細胞内ダイナミックスなどではそうしたシミュレーションも行われている。また、E-cellなど神経細胞に限らない一般の細胞ではそのようなモデリングも行われている。しかし、このようなフルの3次元モデルを用いたシミュレーションは大規模化する場合の通信パターンの問題により、現代のスパコンの隣接通信を使うアーキテクチャーの設計に合致せず、京コンピュータでみるかぎりにおいては数千プロセス並列=数千ボクセル以下程度で限界となるようである。
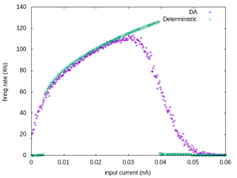
図S4-1 決定論的モデルと確率論的モデル
Hodgkin―Huxleyモデル(deterministic)
での発火頻度とそれをランジュバン方程式化した場合(DA:diffusion aproximation)との発火頻度の比較シミュレーション
サプリメンタリー5:超並列スパコンと神経回路シミュレーション
21世紀初頭までつづいたコンピュータの高速化の歴史は、電子回路の微細化による電力消費の削減分をクロック周波数の上昇にふりわけたことによるものであった。しかし、ある程度以上の微細化が電力消費の削減をもたらさなくなったことから方法論が反転し、クロックダウンして電力削減された回路や計算コアを多数並べることで熱消費を抑えながら計算能力を高めるようになった。このような経緯によって現状の主流のスパコンはCPUとメモリをもつPCのようなノードが多数集まり、ネットワーク通信する分散メモリ型のPCクラスターのようなアーキテクチャーとなった。
ソフトウェア的には 通常の高級言語(C, Fortran, Python, Javaなど) に並列計算用のMPI通信関数ライブラリが付け加わることによって、分散メモリ/計算ノード内でプロセスの並列化を行い、多くの計算コアが使用可能となった。さらに2015年以降の趨勢としてメモリ共有した一つ一つのCPUも数十以上の計算コアをもつようになり、OpenMPディレクティブなど通して、同じメモリを複数のプロセスがアクセスするスレッド並列を組み合わせることが一般的になった。
さらに命令レベルには複数の依存性のない演算や、A+B×Cのような演算を一命令で行うような積和演算を含む並列計算であるベクトル命令(SIMD)を組み込むことでクロックをあげずに計算スピードを稼ぎ、複数の並列化の階層のなかで電力消費低下と性能向上を並列ゆえの性能低下を食い止める両立を行う工夫がなされている。これらを効率よくつなぐためにキャッシュメモリーや通信、さらに高速ストレージ等が使われている。これらを制御するため、現代の並列コンピュータではコンパイラがより多くの役割を担うようになったが、効率的な計算のためには小さい容量のキャッシュメモリーに計算変数をつめこむ必要があり、そのためにはメインメモリー上でも近隣データがまとまっていることが効率的であるなどの課題も生じ、ソフトウェア自動並列性能は理論性能向上においついておらず、コンパイラへのサジェスチョンである付加的ディレクティブや、変数のメモリレイアウト、計算の分割性への配慮やそして高次の通信パターンなどの面倒がふえることになった。

図S5-1 NEIRON K+における主なチューニング
上段 ベンチマーク用神経細胞 カイコガLALのbilateral interneuronでコンパトメント数は3800 ネットワーク構造としては1ニューロンから相対的な決まった位置のニューロンに接続する。
中段 単体性能チューニング 変数のメモリ上の連続化とルーブ順序をそれに沿ったものにすることなので、最適化が進む。
下段 ネットワークチューニング 可能なものはOpenMPを用いたメモリ胸中で通信する。 大規模において直接非同期通信にすることで劣化を緩和する。
しかしながら、このような工夫のもと、トップレベルのスパコン性能は、スパコンにおけるムーアの法則 -2年で性能(もともとはトランジスタ数)が二倍になるを継続しているともいえるが、逆にGPGPUでは旧来のムーアの法則を超えているという主張さえあらわれている。
筆者らが開発しているNEURON K+は、世界的にメジャーな神経細胞シミュレータであるNEURONのBlue Brain Project時のバージョンであるNEURON 7.2をベースにC/C++のソースコードにチューニングを多数ほどこし(miyamot+, 2012; 宮本, 2014)、OpenMPを含むハイブリッド並列への対応、演算負担部分の多いイオンチャネルダイナミクス計算部分の新規書き直しによる変数のメモリーレイアウトの効率化とSIMD化率の改善、キャッシュ効率の向上、シナプス伝達(MPI通信)の通信時間隠蔽など大規模並列化を見据えてチューニングしてきているものである(図S5-1)。
NEURONはマルチコンパートメントモデルに対応し、1990年代から非常によく使われている神経細胞シミュレータである(Hines, 1997)。シミュレーション全体を制御するHOCインタラプタとイオンチャネル等の局所的な計算メカニズムを制御するNMDLというdomain-specific languageコンパイラによってシミュレーションを制御する。NEURONは2005年以降並列化に精力的に対応し、Blue Brain ProjectやHuman Brain Projectでも使用された。
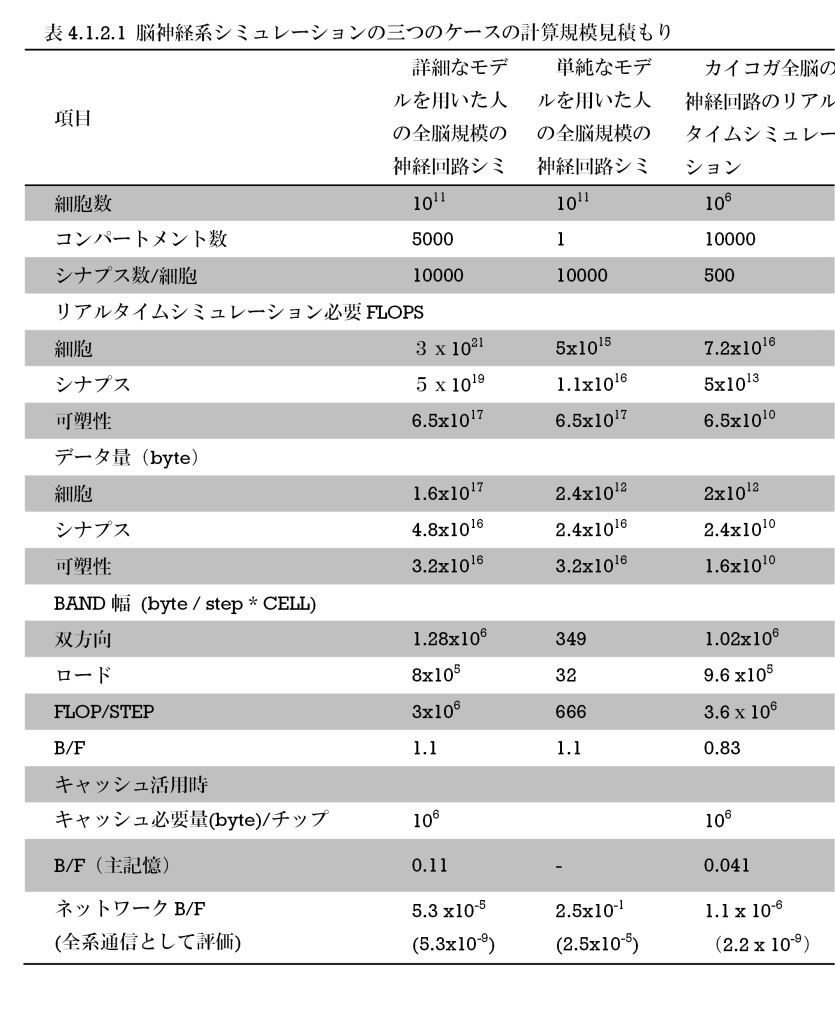
計算方法としては一細胞をケーブルとして近似して電気回路的なケーブル方程式としての計算状態依存のコンダクタンス計算を組み合わせ、ほぼ10マイクロ秒超の時間ステップで計算する。シナプス間の伝達はMPIのメッセージとして表現され、シナプス伝達には1ms程度の潜時があることが並列時の性能低下を緩和する。Izhikevichの見積もりによると(Izhikevich, 2004)、1コンパートメント120FLOPsの計算量だが、筆者らの実測では300FLOPs超であり、360FLOPsとする見積もりにおいて、72PFLOPSの実行速度で昆虫脳全域のリアルタイム実行が可能となる計算になる。これは昆虫脳が哺乳類脳より1神経あたりのシナプス数が少ないことから成り立つ計算であり、人間脳を想定した場合、Leaky integrated-and-fireモデルを採用すれば計算量は減るがシナプスの通信による負荷が膨大なためにそれほど達成目標はかわらないことになる(表S5-1)。
筆者らは、京コンピュータ上で196,608コアの並列実行で187TFLOPSを達成した。また富岳上ではショウジョウバエの20,000神経細胞からなる全脳規模モデルにおいて、細胞形態の縮約や、計算のコア分割などの結果、リアルタイム実行を達成した(図S5-2, Higuchi+, 2022)。
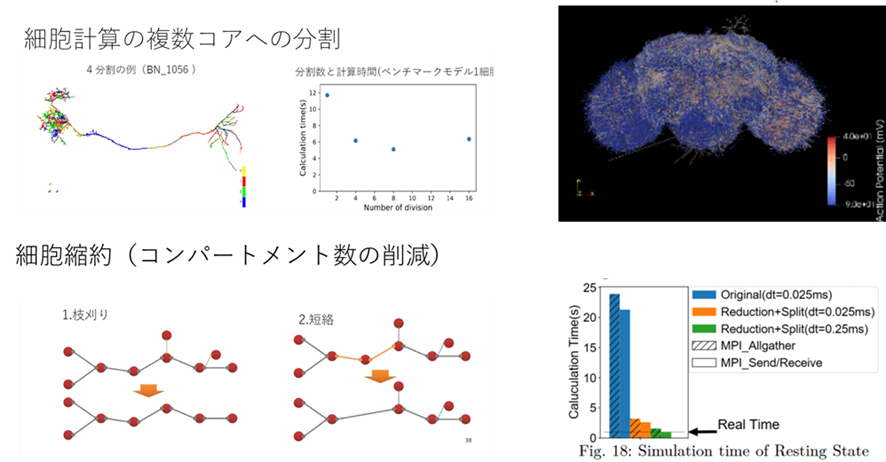
図S5-2 リアルタイムショウジョウバエ全脳シミュレーション
左上)細胞を部位毎に分割することで負荷分散する左下)本質的でない構造を縮約する
ことを更に行う。 右上は20000個神経のシミュレーションから800神経のその電位変化をみせているもののスナップショット。 右下)は計算時間をリアルタイムとの比較とともに示す。(Higuchi+2022)
サプリメンタリー6:昆虫の視覚系(視葉)シミュレーション
昆虫の視覚をまずは振り返ろう。昆虫は単眼とは別に二つの眼をもち、個眼が束になった複眼という構造をもつ。昆虫種によって一つの複眼に含まれる個眼の数は異なり、100個から多いもので10,000程度となる。それぞれの個眼のピント調節機構は脆弱もしくは存在せず、無限遠ピント像のような距離感のない感覚器から昆虫は情報を取り込み、動きの情報をよく活用している。例えば回避行動をおこなうためには物体の立体角と視野上の速度が問題となるが、距離情報はそれほど重要でない(Galbani+, 1999; 山下+, 2011)。
それぞれの個眼に対応して、脳内で視覚情報の処理をおこなう視葉はカラム構造からなり、近隣のカラムと接続されながらも視葉の底までその構造は続く。昆虫の視葉はlamina, medulla, lobula の三層に大別される。ハエの場合、lobula plateといわれる動き情報処理に特化した形態的にはlobulaから分離された領域が存在し、四方向に対応する動きを検知する細胞が存在する。
ショウジョウバエの視葉では電顕コネクト―ムが進み、形状と共に主要神経細胞間のシナプス数まで記録されている。そのシナプス数をシナプス強度と読み替えることにより、神経回路シミュレーションを組むことができる。筆者らは竹村らのコネクト―ムの解析結果(Takemura, 2013, 2017)と、トランスクリトーム(遺伝子解析によりどの細胞腫にどのタンパクが発現しているかを解析する)の結果(Davis, 2020; Davie, 2018)からシングルコンパートメントモデルにより、特に明中心の信号の入力から出力までの部分を再構成した。

図6-1 昆虫の視覚と視葉シミュレーション
昆虫複眼(アリの例: noutomi+2022より) 2ハエ視葉の構造 3電験コネクトームによる視葉明中心動き感知回路の接続推定。 5 T4aにかかる推定的結合
方向感知特性の比較 左 シミュレーション 右 実験(Maisak+2012より)
4 周波数特性と順応の関係
その概要を図6-1に示すが、出力細胞のT4細胞の四つの方向細胞の方向選択性やその周波数測定をおおむね再現することができた。またFFといっても水平的な相互作用は存在する。近接したコラム間では相互抑制と相互興奮がある。特にこの並行した経路における相互抑制は側抑制と呼ばれ、winner take all的に作用する。最終的にはT4細胞に入る寸前の時間遅れのある一定の方向の隣り合ったコラム情報との相互作用が主要な動き検知メカニズムとして機能する。また、非常に基本な刺激に対してはフィードバック神経の仮想的切断実験はあまり影響をおよぼさず、この回路の基本機能はフィードフォワードで説明できたといえる。
最終段では時間遅れのあるシナプス入力があり、これが動き感知として作用する。細胞の応答特の順応が、広い時間特性をかたちづくる(Hayasi et al ., 2022)。
サプリメンタリー7:文字学習シミュレーション
STDPによるシナプス可塑性をマルチコンパートメントH-H型モデルを用い、リカレントネットワーク学習に適用する例として検証してみたものが、文字学習シミュレーションである(図S7-1)。このモデルの入力層では距離空間をつくるため、入力層においては側抑制を含む相互結合のインタラクションを入れている。各細胞はカイコガの触角葉出力神経に近い細胞モデルを実装している。このうち興奮性の結合にSTDP可塑性を付与しランダム結合するネットワークに結合させ、入力に応じてネットワークの一部に報酬の生体アミン信号を模したゆっくりした弱い脱分極を与えている。この実験では8x8のフォント用いて文字情報を与えた。その結果、各部が(文字の)記憶を行う神経回路が形成された。また、動き情報にもある程度対応することも可能であった。
このような相互結合ネットワークは、状態を想起する記憶の場となり、また記憶の痕跡を残す場となる可能性が示されており、昆虫の神経細胞モデルでそのような機能が実現さえたことから、昆虫の記憶機構としても同様のメカニズムがなんらかの形で活用されている可能性が推測できる。

図S7-1 昆虫神経モデルを用いた文字学習するリカレントネットワークモデルの構築
1 ネットワーク構造 赤は興奮性 青は抑制性神経 左入力部で規則構造がある 右はランダム結合。
2トレーニング時には8x8フォントで「かきくけこ」パターンを入力部に提示該当する刺激と同時に出力部の一部に報酬信号をあたえた。
3 報酬エリアの応答 横軸は時間だが、かきくけこの信号を入力部に与えていることを示す。トレーニング後には対応する領域で発火が増える。
サプリメンタリー8:触角葉シミュレーション:昆虫の匂い情報処理一次中枢である触角葉における情報処理
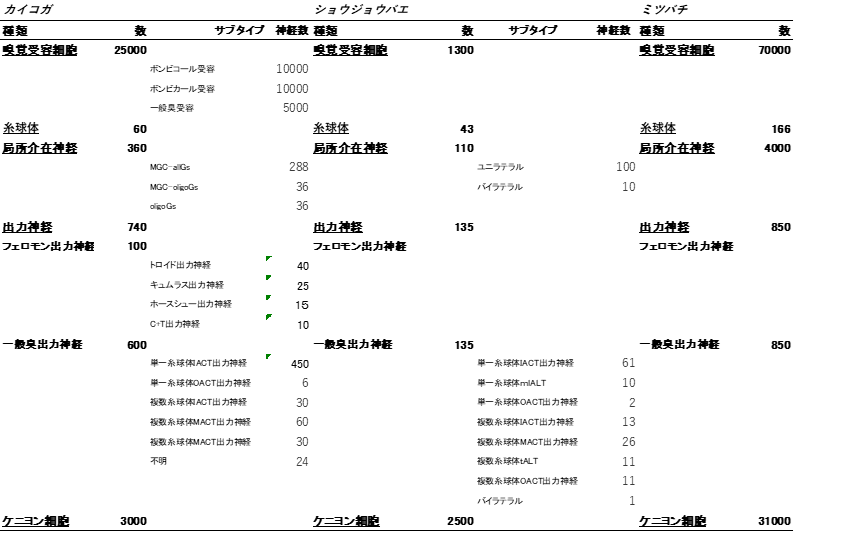
昆虫の匂い情報処理一次中枢である触角葉をみてみよう。昆虫の触角には匂い受容体タンパクが存在する。一つの匂い受容体細胞は匂い受容体一種をもち、同種の多数の匂い受容体細胞が一つの糸球体に収束する。触角葉はすべての匂い受容細胞の出力部出力部が収束している糸球体が球殻状にあつまる構造である。カイコガでは60個、ショウジョウバエでは43個弱、ミツバチでは160個ほどである(表8-1)。カイコガの出力細胞ではあまり匂いの種類に依存した糸球体の位置相関はなく、それぞれの糸球体間の距離を短くする最密構造に近い形で集まっていると考えられる(Namiki+, 2008; Kazawa+, 2009; 図S8-1)。
ガ類の雄には触角葉の触角側に大糸球体(MG; macro glomerular complex)といわれる巨大な構造があり、非常に発達した性フェロモン感受性を支えている。触角葉の神経回路は入力である匂い受容細胞、出力細胞(projection neuron; PN)を局所介在神経(local interneuron;LN)がつないぐ構造をもつ。また、LNは局所的に活動することも報告がされており(Chou Fujwara+, 2014a)、シミュレーションにおいてもLNの単一細胞シミュレーションを行うと一か所からの刺激では多くの場合、細胞全体には活動電位は広がらない(Christensen+, 2001; 図S8-2)。LNは主に抑制性であるために、自己抑制と側抑制の担い手としての働きが大きいが、LN-LN結合があるためより複雑な構造と機能を有している。
例えば触角葉では電位の振動が観察され(Stopfer+, 1997; Okada+, 2001)、個々のLNは匂い刺激に対して興奮性に活動したり抑制性に活動したりする(Matsumoto, 1981)。LNのネットワークには複雑な自律的な活動を支えるポテンシャルがある考えられる。LN-LNネットワークによる振動や個々のLNの応答の違いは、筆者らのシミュレーションでも確認されている(図S8-2)。
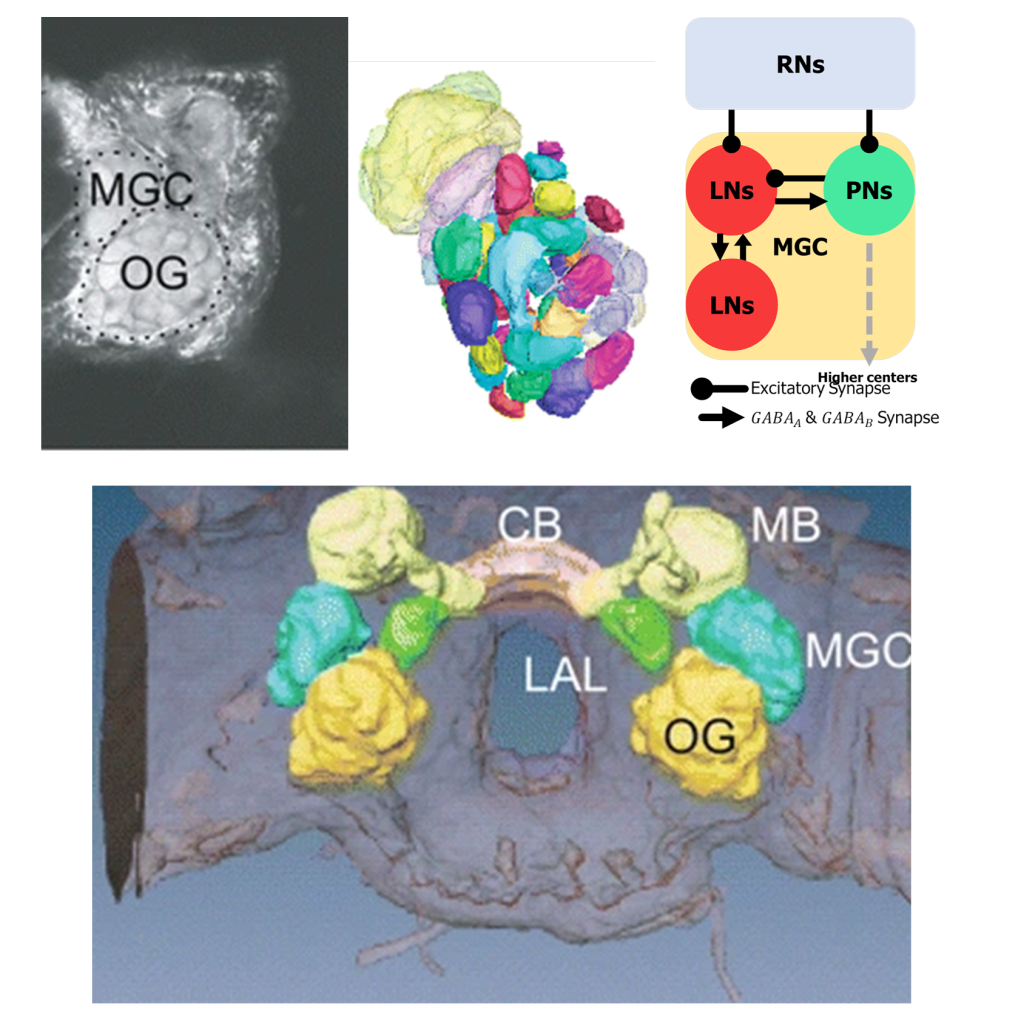
図S8-1カイコガ触角葉
1 共焦点顕微鏡による組織スライス画像 MGC 大糸球体 OG 常糸球体 2スライス画像から3次元再構成した触角葉 3 局所回路模式図 4 脳のなかの触角葉 触角葉はMGC+OG MG:糸球体 CB 中心体

図S8-2 LN40個で構築した触角葉シミュレーションのLNの挙動
左・シミュレーション時の1LNをスナップショットした3次元再構成赤が脱分極側を示す。 LNは部分的に活動している。右 LNの発火頻度の推移の例。
興奮性に応答する場合と抑制応答がある場合がある。本シミュレーションでは確率的にシナプスを生成しているため、どのニューロンが興奮応答でどのLNが抑制応答かは確率的に決まる。なおPNは興奮応答する。
RN→LN間の雑音入力強度を変えたときのLN応答例 (青と緑は同一神経・異なる場所の記録)
雑音入力強度を変えても活動頻度はかわらないため、LN―LNネットワークによる固有振動への引き込みに近い現象が起こっていることが見て取れる。
また、自然界ではメスはフェロモンを断続的なパルスとして放出するが、そのような特性に対応して、フェロモン情報処理におりて濃度感受性の調整が行われていることを筆者らは実験的に見出している(Fujiwara+, 2014)。すなわち、PNに対して触角葉はフェロモンの頻回刺激に対して、その濃度にあった感度調節をおこない、刺激フェロモンの濃度が変化したときはそれに急峻に反応することが実験的に確認された。すなわち、触角葉が刺激履歴に応じた状態を保持し、それとの差を応答として反映させるFristonの理論に大枠は合致するのである。具体的にはシミュレーションと実験を比較することで、LN-LNネットワークが刺激後も活性を保ちながら、PNに対する遅い調整機能(すなわちGABAB受容体経由)によって、このような仕組みを説明できることが判明した(図S8-3)。

図S8-3 シミュレーションによる触角葉の濃度感受性の調節の再現
1 シミュレーションモデル 2 実験(fujiwara+2014b)の結果。1Hzでフェロン刺激の頻回刺激を継続するとPNの応答は次第に一定値にちかずく。 下段左 シミュレーションによる再現PN上での GABAB電流が1HH頻度では減らないことがわかる。 右 上の実験結果のシミュレーションによる再現。(Park +2015)
糸球体からの出力は、単一の糸球体ごと出力されるuPN(ユニタリ糸球体出力神経)と複数の糸球体から入力を受けて出力するmPNに分類される。uPNは、匂い識別出力としての機能の大部分を担うことが推測される。触角葉の糸球体や出力神経の構造や機能から、触角葉は多くの同種の匂い受容細胞からの入力を集約させて感度やS/Nをあげる役割と共に、個々の匂い間のインタラクションにより応答を変化させることで匂いの識別に寄与していることが考えられる(加沢, 2019)。
局所介在神経(LN)は、その構造から複数の糸球体からの入力を触角葉全体の活動として波及し、匂いの組み合わせを特異的に強化する機能を果たす可能性も考えられる。また、糸球体の形態において、よく使われる匂いに対して糸球体の体積が増加する傍証も得られている(Huetteroth+, 2005; Andrione+, 2017)。糸球体を介した側抑制の存在は明らかになっているが、LNは構造機能的に重要な役割を果たすものの、包括的な機能解析には及んでいない。
サブリメンタリー9 嗅覚高次中枢としてのキノコ体とシミュレーション
触角葉の出力はILPC(前大脳側部;inferior lateral protocerebrum)とキノコ体傘部に投射される。AL出力部位であるILPCは、多くの昆虫では形態的特徴から側角(lateral horn)ともいわれるが、ILPCとの区別は明瞭ではないことから、ここではILPCと呼ぶことにする。ILPCは嗅覚情報処理の2次中枢であり、行動パターンを生成する脳内領域であるLALへの神経経路の一部となっている。
キノコ体(Mushroom body: MB)はその名のとおり、キノコのような形をした密集ニューロパイルであり、主にケニヨン細胞(KC)から構成される。個々のKCはキノコ体の傘部で入力をうけて柄部に出力する。キノコ体の破壊実験によって記憶が低下するような実験的証拠から、キノコ体が記憶の座として機能するといわれる(Erber+, 1980; de Belle+, 1994)。傘部には嗅覚以外にも、視覚、味覚、触覚信号などが入力する。ショウジョウバエのコネクト―ムから、ショウジョウバエではMBに視覚入力がほとんどないといわれているが、傘部周辺には入力しているので大意としては入力があるともいえる(Vogt+, 2020; Li+, 2020)。
柄部は枝分かれしており、その周辺部分とインタラクションがある。MBONは柄部から様々な脳内の場所に出力するキノコ体の出力細胞である。ショウジョウバエにおいて34対のMBONが同定されてる(Aso+, 2014)。キノコ体柄部の特定の部位から入力を受け、脳内の様々な領域に投射する。柄部にはループ構造や柄部から傘部への巨大フィードバック神経も存在する。このような構造から、MBのような高次中枢からの多領域の活動が監視し、昨日修正を行う働きのあることが推測されている(Wessnitzer+, 2006)。また、柄部ではその周辺の神経細胞との相互作用が推定され、特に報酬/罰に関連する生体アミン系神経細胞の出力が柄部に入力することはよく知られている(Rubin+, 2014)。MBON間でループ結合が報告されており(Ichinose+, 2015; Lindsey+, 2020)、MBONへの入力部位においてSTDPが起こることも確認されている(Cassenger+, 2007 )。

図S9-1 嗅覚高次中枢としてのキノコ体とシミュレーション
1 触角葉からMBに至る回路シミュレーション全体の接続模式図。 ORNからALの入力された匂い信号はLNとmPNによって調整された後にキノコ体にuPNによって出力される。KCはMBONに出力するがそのときDAN(ドーパミンニューロン)による報酬信号による修飾をうける。MBONへの接続とその周りのループ構造は葉部の部位によって異なる。
2 レセプター応答はyao+2005のものそのまま近似してポアソンスパイクとしてALに
入力される。 PN応答はkazama+2009に合うようにPNの性質をフィティングした。
LN応答は seki+2010の報告をもとにLNの性質を決定した。
3 上段はKCからMBON6へのシナプス強度の推移 下段はMBON6でのスパイク頻度を示す 右に示すように報酬によってMBONへの伝達が強化されて応答が大きくなる。
筆者らはこの嗅覚系の触角葉からキノコ体出力までの神経回路を、ショウジョウバエ光顕コネクトームのデータを用いて再現し、シミュレーションをおこなった(図S9-3, Higuch+, 2022 )。これまでに報告されている触角葉における神経応答を再現するように触角葉のモデリングを行い、コネクトームデータに基づき、KCまでの神経接続を再現しシミュレーションを構築した。
このシミュレーションにおいて特定の匂いに対して報酬系(たとえば甘いという信号)を作動させることで、MBONの応答がSTDPにより増大することが示され、味匂い連合学習の中核となる学習がおこることを再現することに成功した(Higuchi+, 2022)(図S9-1)。このように特定の行動実験に基づく特定の学習を詳細モデルによって再現する道が拓かれたといえる。
Arenaらは、キノコ体から触角葉に戻るフィードバック神経(Hu+, 2010)が記憶機能において大きな役割をはたしていると考えている(Arena+, 2012)。 キノコ体から触角葉に戻るループにより、リカレントネットワークの系となり、系全体として連想記憶回路を構築する可能性が示唆される(図S9-2)。匂い受容体に対する応答が安定した後、系へのノイズ刺激により直前に与えられた信号処理のメモリー痕跡が再生されることを示している。これは脳に記録された匂い記憶のリコールであり、行動評価がおわった後に記憶をリコールし、報酬信号により特定の匂いに対する行動が強化される仕組みと考えられる。

図S9-2 AL―MBリカレントネットワークモデルの学習シミュレーション
左 ネットワーク経路 ALはMBのKCに信号をおくり、ALニューロンは3x3で構成して列に相互抑制をもち、異なる列のものには横軸には可塑的な興奮をもつ、MBのスパース性を反映してKCは10x10でかつ、近隣の細胞と可塑的な相互興奮、そして全体抑制をもつ。MBからALには巨大なフィードバックでつながれるか、この神経も可塑的である。すべてのニューロンはIzhikevichモデルでつくられた。 ALに刺激を与え続けると、MBでは自己組織化がおこり、クラスター化する。 この状態では列にひとつずつ発火する近い組みあわせのALニューロンが発火する(赤部分が追加される)さらに ある程度学習させたネットワークのMBニューロンに白色ガウス電流をあたえるとALで直前の匂い応答に近いものを想起する。